Tomas Rokicki (rokicki@gmail.com) and Gil Dogon (gil.dogon@mobileye.com)
Our previous work extended the calculation of near-optimal rulers based on affine and projective planes through 40,000 marks. These constructions generate the best known rulers for all sizes in excess of 16 marks; to our knowledge, despite significant interest, no one has been able to find any Golomb ruler with more than 16 marks with length less than the best of that generated by the affine or projective plane construction. This leads to hypothesis A:
Hypothesis A: for all n > 16, the optimal Golomb ruler can be generated by an affine plane or projective plane construction.
No counterexample to hypothesis A is known despite a great deal of CPU expended over the past several decades, not the least of which was the distributed.net's OGR-24 through OGR-28 efforts which have consumed thousands of CPU years over the past 16 years. Also, the search for Golomb rulers has been a central problem for constraint-based search for some time, with no counterexamples found.
The final length of the best rulers found were in general very close, and slightly less than, the number of marks squared. Rulers with n marks and of length less than n2 are called subquadratic rulers. Previous work by Dimitromanolakis showed the existence of subquadratic rulers through size 65,000. This leads to hypothesis B:
Hypothesis B: subquadratic rulers exist for all n.
One measure of how good a Golomb ruler is, is how much better than quadratic it is. Let us define the quality b(R) of a ruler R with n marks and total length d as n-sqrt(d). If OGR(n) is the optimal Golomb ruler of length n, then assuming hypothesis B is true, b(OGR(n)) is positive for all n. Another question of interest is, how large can the quality b(OGR(n)) be?
Hypothesis C: b(OGR(n)) is unbounded.
This hypothesis was conjectured by Erdös and Turán in 1941.
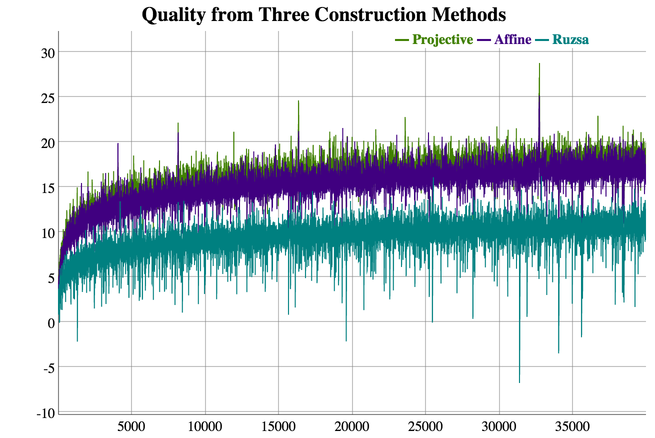
The following two images and interactive graphs summarize the quality results we obtained for the three construction methods through rulers of size 40,000 marks. Click on the images for an interactive graph; select-drag a region to zoom in, and double-click to zoom back out.
Using the programs created for our previous work, we set out to explore these hypotheses for larger values of n. First, we tried to extend the work of Dimitromanolakis past 65,000. There are three known asymptotically-optimal algebraic constructions: the Ruzsa construction, the affine plane construction, and the projective plane construction. The first two construction methods have very fast (linear time) modular ruler construction methods (Ruzsa trivially, the affine construction [see Lindstrom below]), but for the projective plane ruler construction only a quadratic algorithm is known. The affine plane construction usually generates better rulers than the Ruzsa construction, so we use that as our main workhorse. We did not consider all possible derived Golomb rulers but only scanned a modular Golomb ruler until we showed the existence of a subquadratic ruler for all sizes in the range between the generating prime power and the previous prime power. This very quickly covered the entire range from 40,000 through to 500,000 except for about eight gaps between prime powers.
For the larger gaps that caused more problems, we started with the projective plane construction rather than the affine plane construction; even though generating the modular ruler takes longer for the projective plane construction, the actual scanning of the derived rulers, which is has the dominant run time (cubic in n) can be done more rapidly.
When generating derived modular rulers from a given modular ruler, you multiply the original ruler by a value m that is relatively prime to the modulus of the rulers (and the multiplication is done modulo the modulus) and then sort the resulting values. So for instance, for the projective plane construction, with a prime of 13, the modulus is 132+13+1 or 183, which is factored into 3*61. You would consider rulers generated by multiplying the original rulers by the values 2, 4, 5, 7, 8, 10, 11, and so on. The multiplication, remainder, and the sort operations are the most costly operations in the scan when you are focused on a small range of final Golomb rule sizes; we were focused on only the small range for which we had not already found subquadratic rulers.
Rather than considering the distinct multipliers sequentially, you can instead consider them in a sequence that emphasizes multiplication by small integers, especially 2 or 3. Given an already sorted set, you can perform multiplication, modulo, and sorting by such a small integer much more rapidly than the naive implementation. For the multiplication and modulo steps, you can instead use addition and subtraction, where the value to be subtracted changes only a small number of times throughout the range. The sort step can be done by merging a small number of already-sorted subranges. For instance, given the projective-plane-derived modular ruler
0 1 8 24 37 41 59 107 119 128 134 139 153 181
with the modulus 183, multiplication by two gives
0 2 16 48 74 82 118 214 238 256 268 278 306 362
The value to subtract to keep it in range is 0 for the first half (through 118) and then 183 for the rest, giving us
0 2 16 48 74 82 118 31 55 73 85 95 123 179
The sort step is just a simple merge of the two sorted subsequences, giving
0 2 16 31 48 55 73 74 82 85 95 118 123 179
For projective-plane-derived rulers, the modulo for a prime power p is p2+p+1, which is never divisible by 2, so most of the time the generation of the next derived ruler can use the multiplier 2. For affine-plane-derived rulers, the modulo for a prime power p is p2-1, which is usually divisible by 2 (except for when p is a power of 2) and usually divisible by 3 (since p2-1 is (p-1)*(p+1) and since p is usually not divisible by 3, one of p-1 or p+1 usually is) so the smallest multiplier we can frequently use is 5, and thus turns out to be significantly slower (at the sort/merge step) than 2.
For the example above, with p=13 and a modulus of 183, we only ever need use a multiplier of 2, as the first 20 powers of 2 mod 183 generate all necessary multipliers:
1 2 4 8 16 32 64 128 73 146 109 35 70 140 97 11 22 44 88 176
(The other 100 multipliers that are relatively prime to 183 generate equivalent rulers by symmetry; we omit the details.)
So even though generating the original modular Golomb ruler is slower with the projective plane construction, if we plan to scan a significant fraction of the possible generated rulers, the projective plane construction ends up being faster. Another benefit was the projective plane construction typically (about 2/3rds of the time) generated slightly shorter rulers.
So for the gaps that turned out to be difficult, we used the projective plane construction. With this, we were able to cover all but one gap in the range through 500,000. The remaining gap was 492,116 through 492,118. In order to fully explore the projective plane construction, we had to construct all 39 billion possible different modular rulers and scan each of them for potential solutions. Next, we did the same for the affine plane construction, constructing and scanning all 10 billion possible different modular rulers. None of them were subquadratic for the three target mark counts given above.
This result is not completely surprising; the gap between the consecutive prime powers 492,113 and 492,227 is 114, which is a maximal gap (the first gap of that size or greater in the sequence of prime powers). The typical prime gap for primes around this size is ln(p) or about 14. (The projective plane construction for p=492,113 constructed subquadratic Golomb rulers for 492,113 and 492,114 marks.) Empirically, we see that the projective plane and affine plane constructions typically create subquadratic rulers only for values close to the prime power used to generate them (and for some trivially small values); for this maximal prime gap, the size of the prime gap was too large to span.
We did not evaluate the next prime power up (492,251) for this range because of the computational time required and because we believe it is extremely unlikely to generate subquadratic rulers that small, based on the relationship between the size of the range of subquadratic rulers generated and the prime power used to generate them.
So we have found for all sizes through 492,115 marks, a subquadratic Golomb ruler exists; for all sizes through 500,000 marks, only three values (492,116 through 492,118) do not have a proven subquadratic ruler. In addition, one of the following must be true:
Hypothesis A is false; there is some subquadratic ruler for 492,116 that is not generated by the projective plane or affine plane construction;
Hypothesis B is false; there is no subquadratic ruler for 492,116;
A subquadratic ruler for 492,116 can be constructed by the projective plane or affine plane construction for a prime power of 492,251 or greater.
Some bug exists in our programs. We have worked hard to avoid this, including completely separate implementations and comparing results.
We believe one of hypothesis A or B is false.
There has been much attention in the literature to using general optimization and search techniques to find Golomb rulers. So far these techniques have been shown to be effective only for a very small number of marks (through 16 to 20 marks), far short of the 492,116 marks we are interested in. Alternative algebraic or algorithmic construction methods are significantly inferior to the projective plane or affine plane construction (with the exception of one method, the Rusza method, which is only somewhat inferior and which we have also explored for the range in question without finding a subquadratic ruler).
Despite great interest, no construction techniques of comparable effectiveness have been found (the projective plane and affine plane construction techniques date back to 1938 and 1941, respectively).
We now turn our attention to hypothesis C. Empirically we have found that powers of two greater than 210 generate rulers with the largest b(R). We do not yet have an explanation on why powers of two generate better Golomb rulers. The symmetry of the set of derived rulers for g=pn has order 4n (for the affine plane construction) and 6n (for the projective plane construction) and n is higher for the powers of two, so there are even fewer derived rulers to explore, and thus we would expect slightly worse rulers to be found. Yet, consistently, powers of two find Golomb rulers of higher quality than other prime powers; every record quality (by increasing n) between 4,000 and 40,000 was found by the affine or projective plane constructions starting from a modular ruler derived from a power of two.
We assume this continues for values of n greater than 40,000. We focused on these rulers to try to extend the known best b(R). We explored modular rulers of size 216=65,536 through 221=2,097,152. Since our purpose was to opportunistically look for rulers of high quality, rather than to prove an optimal quality, we only considered derived rulers (sub-rulers) whose length is close to the power of two (within 110). Further, for rulers larger than 32768, we only considered the projective plane and affine plane constructions (though we have not yet run the affine plane construction for sizes 220 or 221). The number of rulers searched grows exponentially with n (by approximately a factor four), as for 2n , we have searched the full range of inequivalent possibilities for a modular ruler, which is phi(22n+2n+1)/6n in the projective case, and phi(22n-1)/4n in the affine case (PHI is Euler's totient function).
For the largest size, we were able to find a Golomb ruler at n=2,097,125 marks of length 4,397,762,317,463, for a b(R) of 40.758. Based on this result, and how much larger this is than the b(R) values for rulers smaller than 40,000, we suspect that b(OGR(n)) is indeed unbounded.
Record qualities by prime powers of two (question mark means we did not run the affine construction).
| g | n | d | b(R) | type | # rulers |
|---|---|---|---|---|---|
| 2048 | 2046 | 4124805 | 15.04 | aff | 60016 |
| 2048 | 2046 | 4118063 | 16.70 | proj | 54498 |
| 4096 | 4084 | 16517156 | 19.87 | aff | 138240 |
| 4096 | 4091 | 16583409 | 18.73 | proj | 139968 |
| 8192 | 8182 | 66601079 | 21.05 | aff | 859950 |
| 8192 | 8177 | 66501869 | 22.13 | proj | 728208 |
| 16384 | 16371 | 267316415 | 21.19 | aff | 2370816 |
| 16384 | 16367 | 267074038 | 24.60 | proj | 1820448 |
| 32768 | 32750 | 1070915788 | 25.15 | aff | 8910000 |
| 32768 | 32756 | 1071073269 | 28.74 | proj | 11748240 |
| 65536 | 65515 | 4288124720 | 31.23 | aff | 33554432 |
| 65536 | 65523 | 4289307076 | 30.20 | proj | 23224320 |
| 131072 | 131042 | 17162400535 | 36.65 | aff | 168424950 |
| 131072 | 131033 | 17163471622 | 33.57 | proj | 142888536 |
| 262144 | 262125 | 68691708709 | 33.97 | aff | 362797056 |
| 262144 | 262122 | 68685856466 | 32.13 | proj | 424189440 |
| 524288 | 524252 | 274802524432 | 35.90 | aff | 2411191314 |
| 524288 | 524242 | 274803720226 | 34.75 | proj | 2066689584 |
| 1048576 | aff | 5921280000 | |||
| 1048576 | 1048529 | 1099332551684 | 38.39 | proj | 4704480000 |
| 2097152 | aff | 28901432448 | |||
| 2097152 | 2097125 | 4397762317463 | 40.76 | proj | 34426570752 |
P. Erdös and P. Turán, On a Problem of Sidon in Additive Number Theory and on Some Related Problems
James Singer, A Theorem in Finite Projective Geometry and Some Applications to Number Theory
Konstantinos Drakakis, A Review of the Available Construction Methods for Golomb Rulers
Apostolos Dimitromanolakis, Analysis of the Golomb Ruler and the Sidon Set Problems, and Determination of Large, Near-Optimal Golomb Rulers
B. Lindström, Finding finite B2-sequences faster, Mathematics of Computation, 67 (1998), 1173-1178.
I. Z. Ruzsa, Solving a linear equation in a set of integers I, Acta Arithmetica, LXV (1993), 259-282.